Running the Relativistic Simulation

using the Twins with no Instant Velocity Change example

This tutorial is an extension of the Twins tutorial. It examines the behavior of time and distance for a Twins example with a realistic change of velocity during the astronaut’s turnaround.

Please Note: Relativity is built on and modifies Newtonian Physics. These tutorials do not attempt to teach the user Newtonian Physics. They assume the user already knows Newtonian Physics.

If you have not already gone through the regular Twins tutorial you should. That tutorial may be found at http://relativitysimulation.com/Tutorials/TutorialTwins.html. This tutorial assumes you have a level of familiarity with the application that you will have gained by running that tutorial. All of the tutorials and the simulation application itself are accessible at http://relativitysimulation.com. This tutorial does not implement relativistic acceleration. It approximates the consequences of relativistic acceleration using a series of small reference frame transformations. (Acceleration will be implemented in a later version of the Application.)

Selecting the Predefined Example

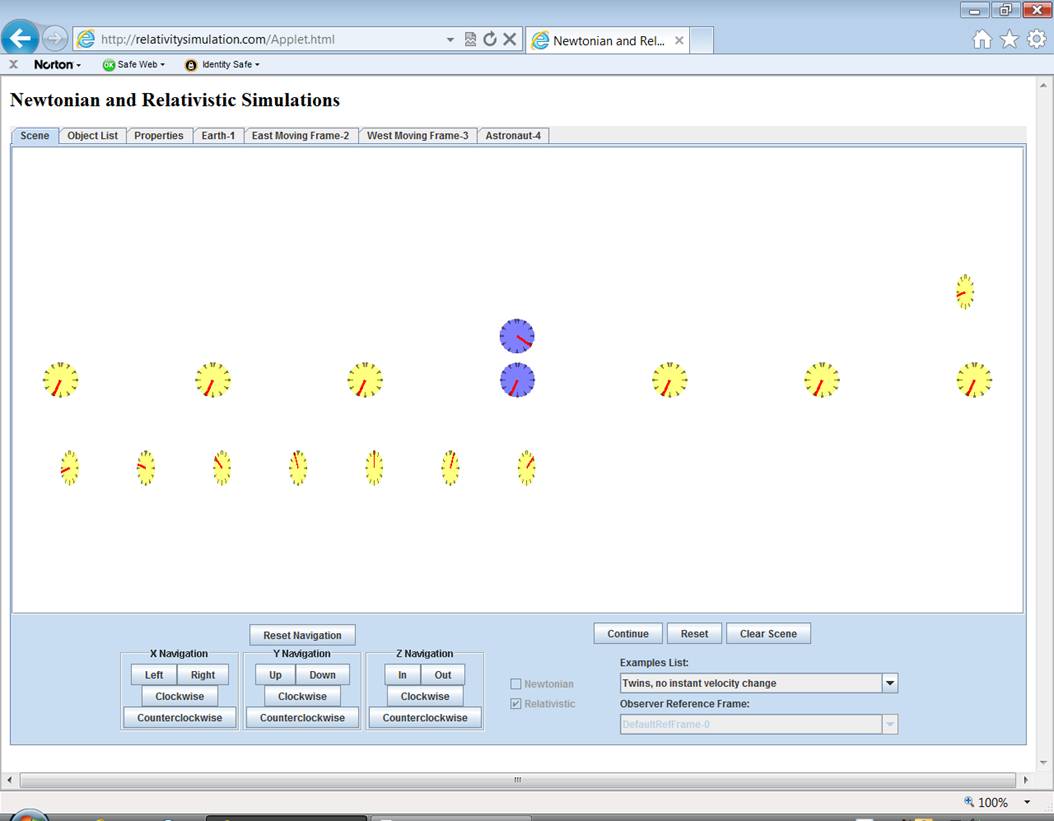
Select “Twins, no instant velocity change” from the Examples List.

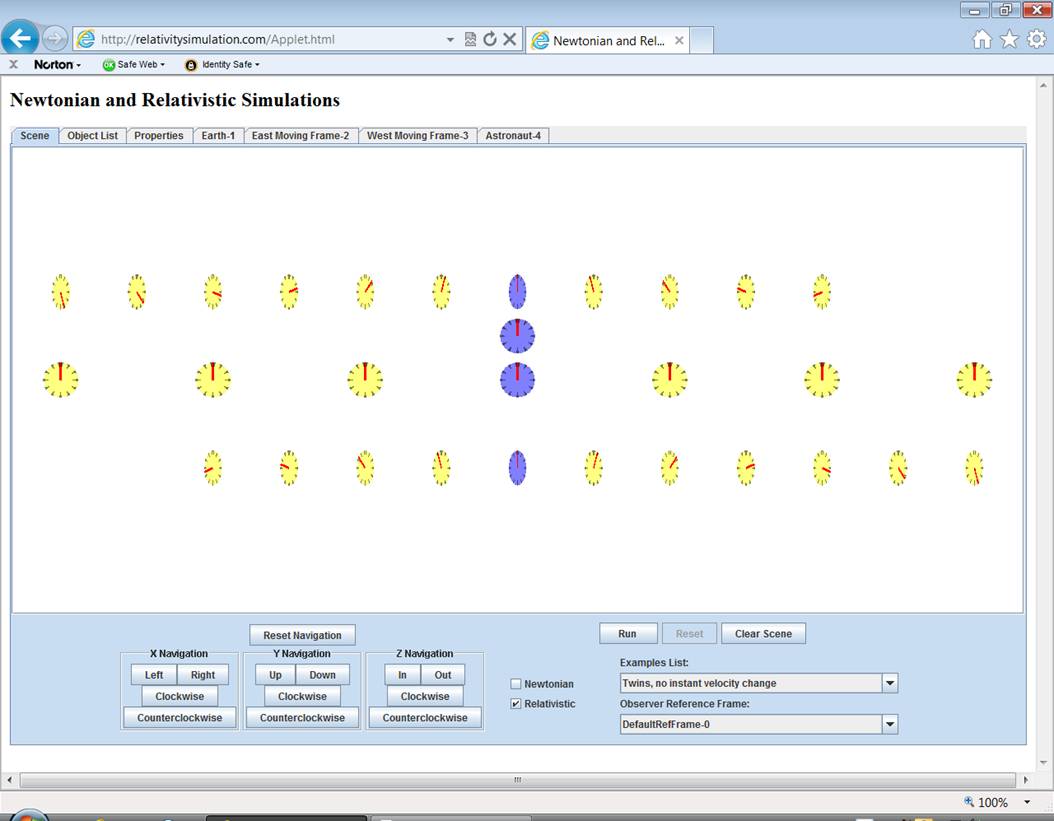
The scene looks the same as that for the regular Twins example. And just as with the regular example you should zoom In or Out till the scene on your computer looks like the one pictured below.

Running the Example

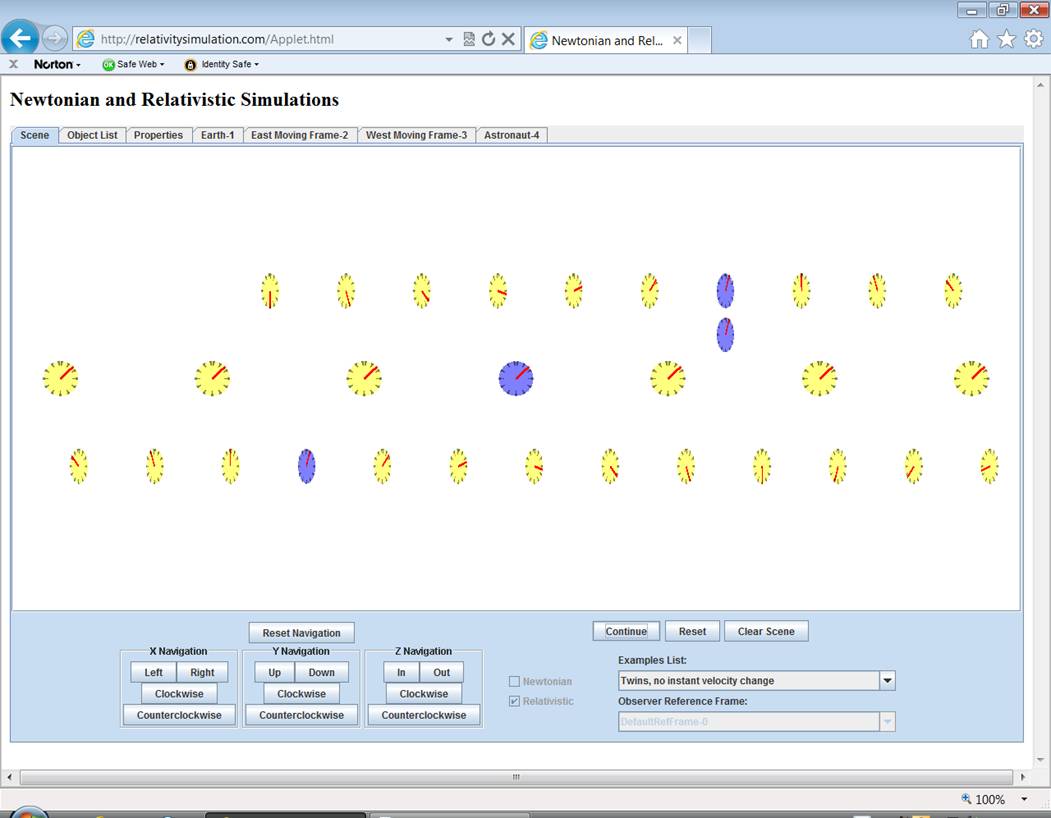
When you run this example you will see the same behavior as the Twins example with the following exceptions. During the astronaut’s turnaround instead of a single jump from a reference frame moving at relativistic speed to the right to a reference frame moving at relativistic speed to the left, the turnaround will be done in increments. That will consume a little extra time and distance so that the reunion times on both twins’ clocks will be different from the regular Twins example.

Switching Reference Frames

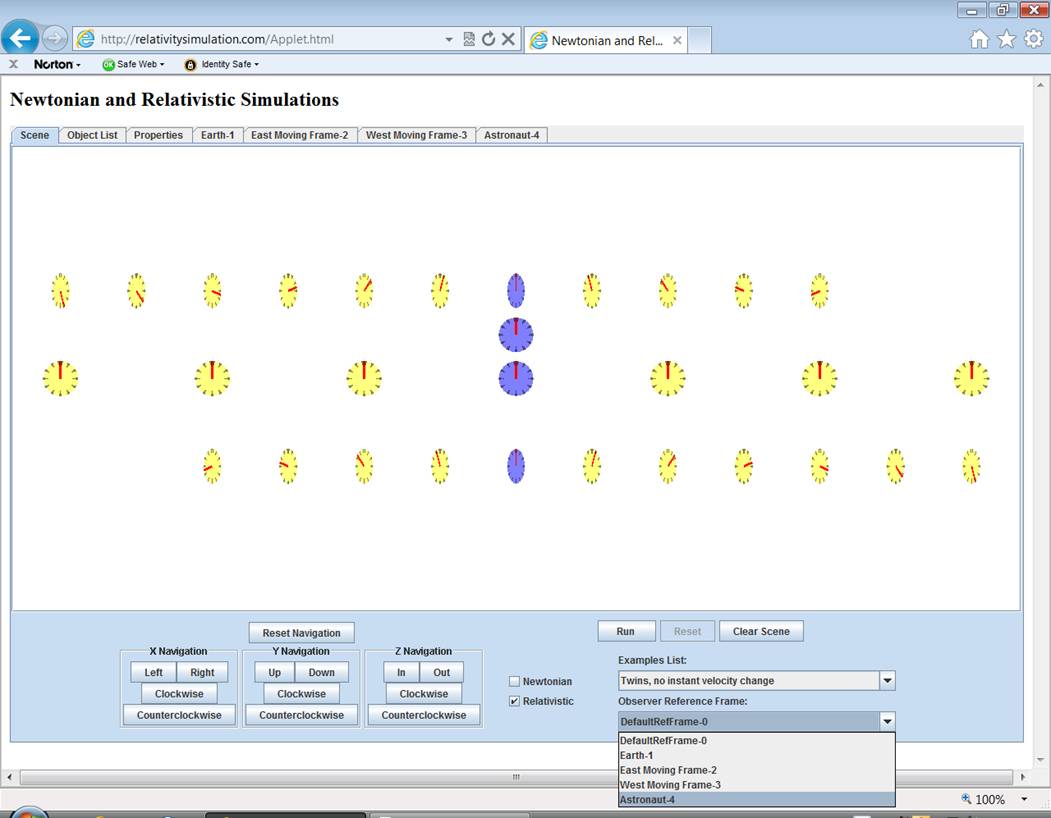
The value of this example is the behavior you see when running with the astronaut as the observer reference frame. So switch reference frames to Astronaut-4.

Run the example several times concentrating on the behavior of the Earth clock during the astronaut’s turnaround.

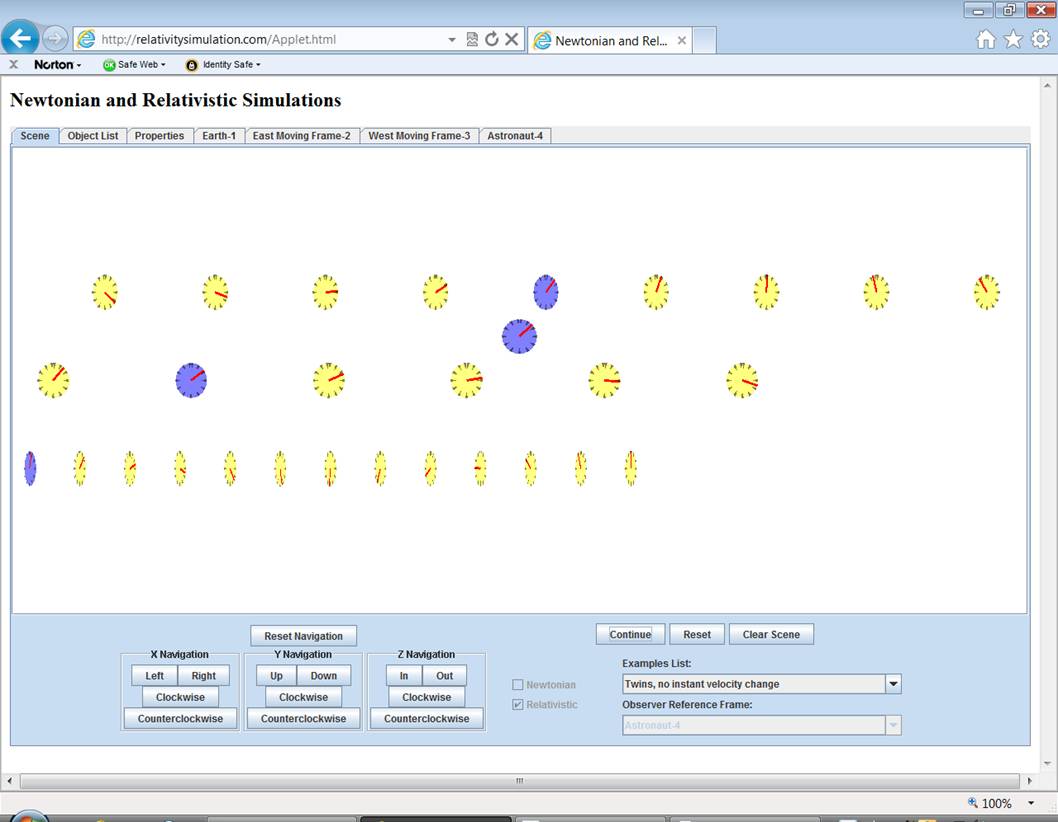
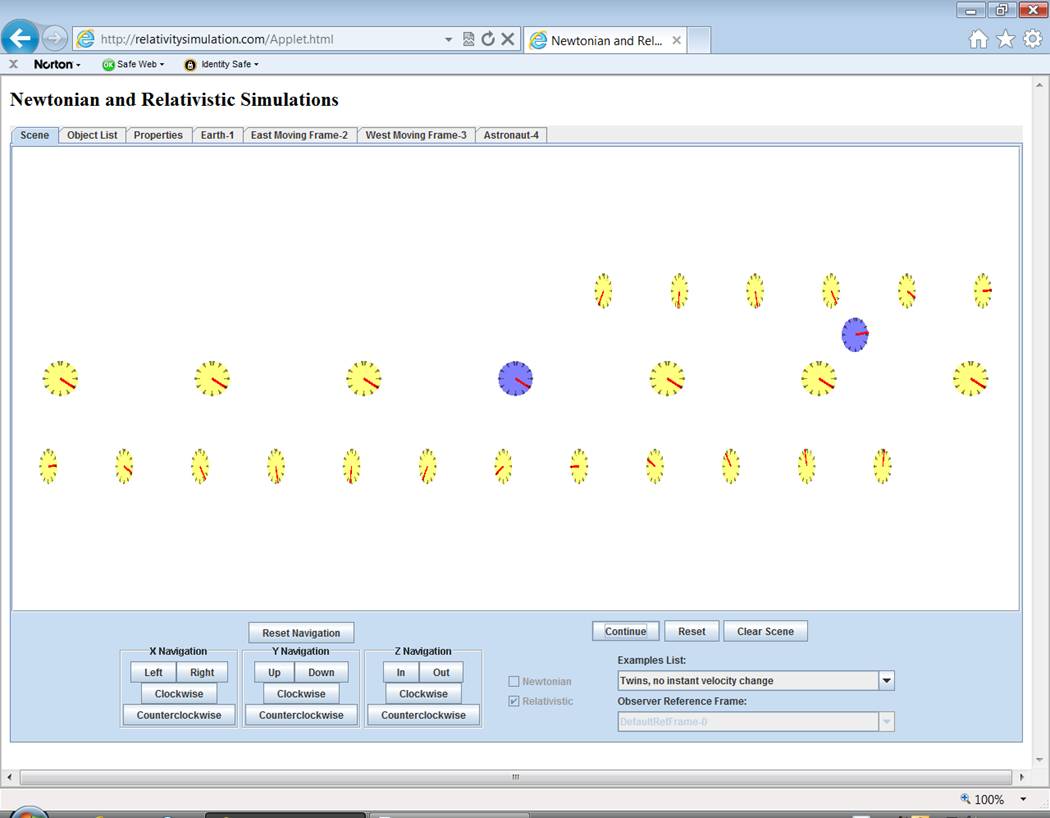
Notice that the length contraction of the row of clocks in the earth reference frame first loses its contraction and then regains it. In order to turn around, the astronaut must shrink relative velocity and come to rest in the earth’s reference frame, then regain relative velocity in the opposite direction. So length contraction of objects in that reference frame first goes away and then comes back.

Also, instead of jumping, the earth clock appears to run fast, in a choppy sort of way. (When real acceleration is implemented it will be a smooth, fast running clock.) The speed of the earth clock is so fast compared to the astronaut’s clock that it catches up to and passes far ahead of the astronaut’s clock.

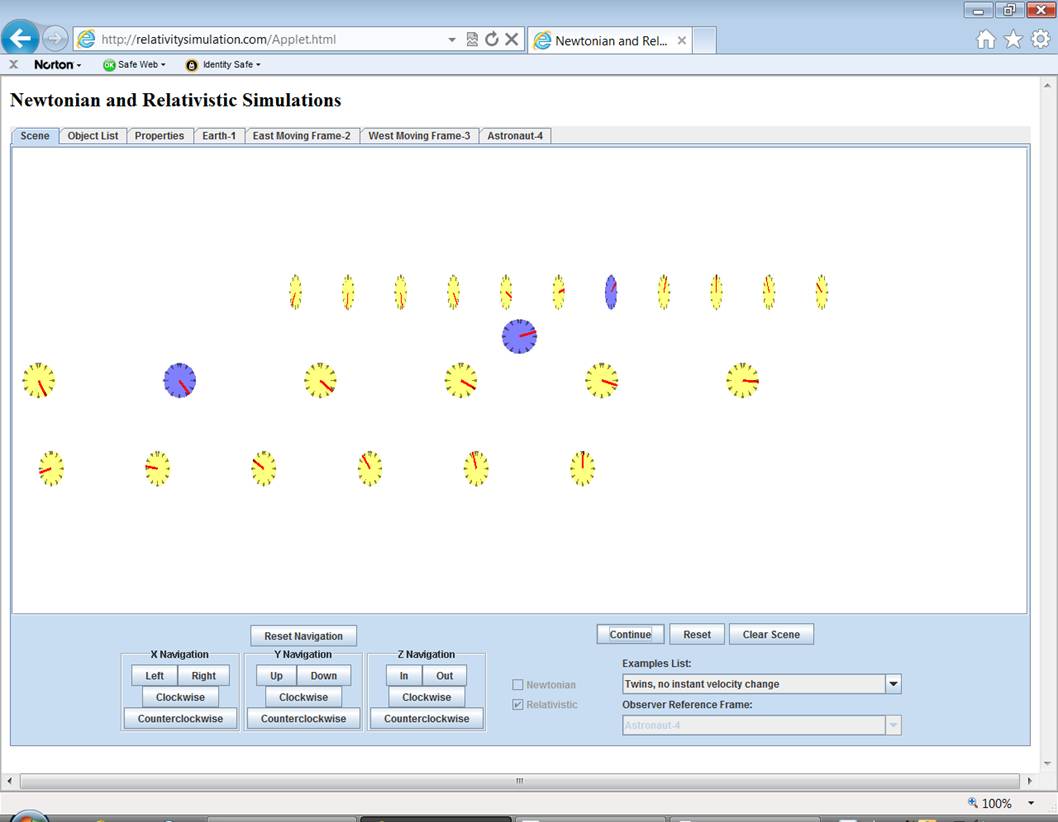
After the turnaround, it is so far ahead that even its slower running during the return trip is not enough and the trip ends with the earth clock reading ahead of the astronaut’s clock. This situation (the other guy’s clock running faster) will only occur when considering the example from the reference frame of the accelerating astronaut. In Special Relativity an inertial observer will always consider a clock on a body in another reference frame to be running slow, whether the body is accelerating or just coasting in an inertial frame of its own. But an accelerating body will always consider the clock on an inertially moving body to be running fast. And that’s the real resolution of the Twins Paradox.

Further Experimentation

There are two examples and tutorials where the astronaut and earth exchange light signals. Exchanging light signals is a way for the twins to prove who is aging faster without having the astronaut land back on earth and compare clocks.