The Train and the Lightning

A train whose passengers believe is meters in length is moving along a track at speed .866c with respect to an observer at the station. (.866c is .866 times the speed of light) The observer determines that two lightning strikes have hit the train and track at the same time. Strike A scorched the track and the back of the train. Strike B scorched the track and the front of the train. Since the train is contracted by 50% to the observer at the station, he records the lightning strikes to be meters apart. If we compare and contrast the lightning strikes between the passengers on the train and this observer, will we find a contradiction? I say no. But lets crunch the numbers and see.

The problem has been given from the point of view of the observer at the station. The point of view of passengers on the train can be determined by switching reference frames. To do that we need to define two reference frames. The observer at the station is one reference frame. Lets attach his coordinate axes to the tracks with the x-direction pointing down the tracks. The train is the other reference frame. Lets attach its coordinate axes to the back of the train with the x-direction pointing toward the front of the train. The usual setup is to declare that the two axes coincide at the start, call it time t=t’=0. For our problem we may declare that the lightning strikes occurred at t=0. That’s the time as determined by the observer at the station. Each reference frame may be considered to have relative velocity .866c with respect to the other. First calculate gamma for the relative velocity. I picked a speed that makes for an easy value of gamma.

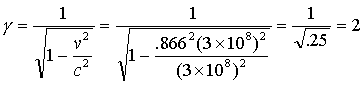
Now use the Lorentz Transformation to transform the station coordinates (t, x) to the train coordinates (t', x') for the two events.

Event A, lightening strikes back of the train and track:

Event A (0, 0) for the observer in the station transforms to A' (0, 0) for the passengers. So the passengers on the train record lightning scorching the back of the train and the track at position 0, time 0 in their reference frame.

Event B, lightening strikes the front of train and track:

Event B (0, ) for the observer in the station transforms to B' (-.866, ) for the passengers. See calculations below.

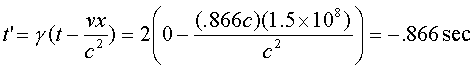
Passengers on the train record lightning scorching the front of the train and track (that’s meters from the origin of their reference frame) at .866 seconds before the strike at the back.

It takes some time for the implications of this calculation sink in. Think about it. Passengers on the train consider their train to be meters long. The observer at the station understands that even though he measures it at half that length. Passengers on the train have dutifully recorded that lightning scorched the front and back of the train, though not at the same time. If the observer at the station believes in Special Relativity, he understands that two events that are simultaneous in his reference frame may not be simultaneous in some other reference frame. Now think about the scorch marks on the tracks. As far as the passengers on the train are concerned, the track is passing under them at a speed of .866c. And it is the track length that is contracted by 50%.

Let the passengers on the train do some straightforward Newtonian physics. (It’s OK if they know which parts of Newtonian physics still apply.) They record the first scorch mark on the track at -.866 seconds and meters from the origin of their reference frame. The other scorch mark has not yet been created. The track and the first scorch mark are speeding under the train toward the back and the origin of their reference frame. By the time the second scorch mark is created at the back of the train, .866 seconds have elapsed. Since distance is speed times time, the first mark has passed (.866)()(.866 seconds) = meters under the train. So it is only meters away from the back of the train when that second mark is created. Both marks then recede into the distance behind the train with that meter separation.

Now if the passengers on the train believe in Relativity, they will have no problem believing that the meter separation of scorch marks they just observed means a meter separation to any observer at the station. Just like the observer at the station believed that the meter length he observed for the train meant a meter length to passengers on the train.

If someone on the train wants it to turn around, go back to the station and stop for a face-to-face, touch-it, feel-it comparison, that’s OK. The length between scorch marks will be m on the train (front and back) and m on the tracks. Exactly what everybody expects.

Note that the calculations were all made with no regard to an absolute length, absolute motion or absolute time. Instead of stopping the train, we could accelerate the station/tracks to catch up with the train and make the comparison in the reference frame of the train. Same results.